クラスタリング

このセクションの他の記事

クラスタリングの使い方

クラスタリングとは、データを類似性に基づいてグループ（クラスタ）に分割する手法です。各クラスタ内のデータは互いに類似しており、異なるクラスタのデータとは異なっていることを目的とします。クラスタリングは、機械学習やデータ分析において広く利用されています。

ClusterFlowを用いることで、クラスタリングの学習が行えます。

■使い方

使い方の説明用に、プロジェクトテンプレート「センサーデータによる異常検知」の改変したデータセット使って、MatrixFlowのクラスタリング機能を紹介します。

【データセット概要】

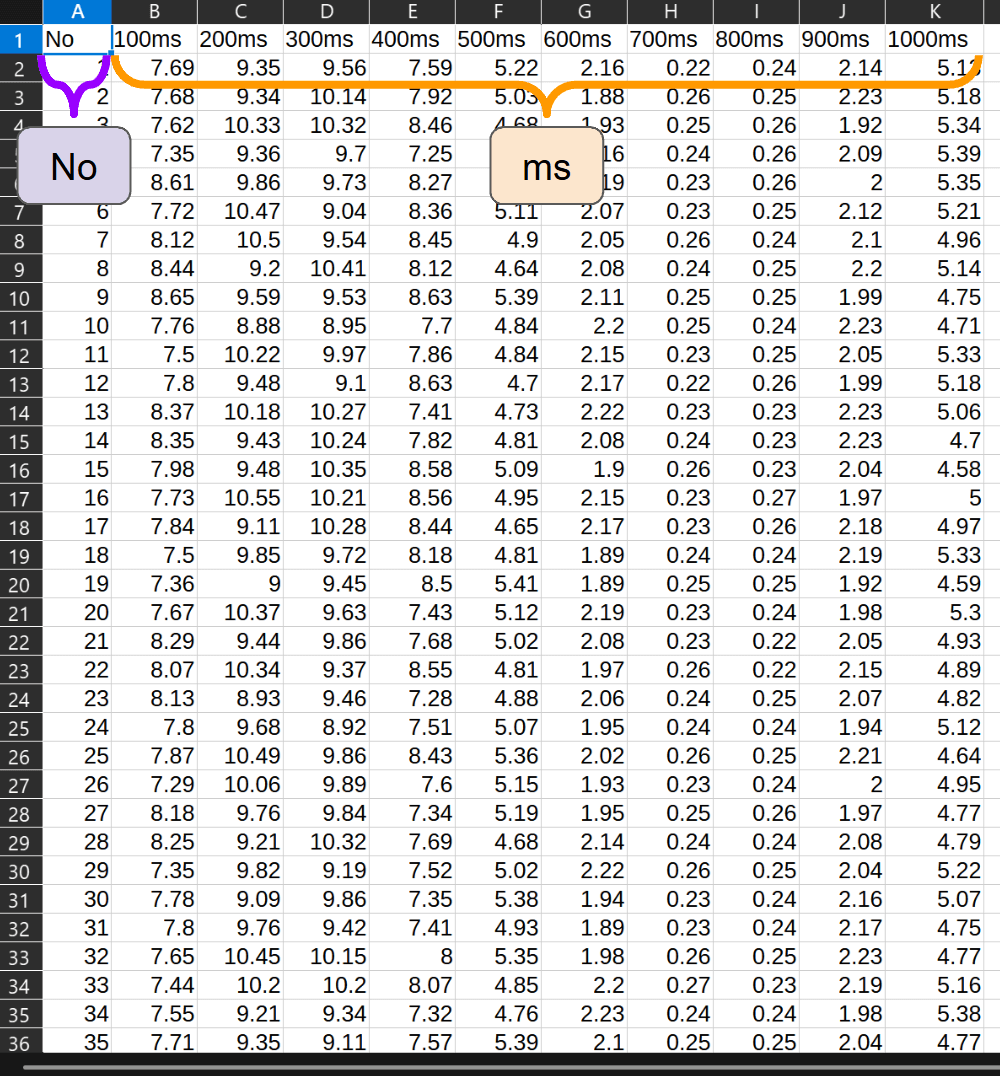
本データセットは、1000msを1周期とする波形データを、100msごとに数値化したデモ用データです。
このデータセットは以下の列で構成されています。

　No：各レコードを識別するための一意の連番
　ms列（10列）：各時刻における波形の数値データ – 100ms、200ms、300ms、400ms、500ms、600ms、700ms、800ms、900ms、1000ms
各レコードには、1周期分（1000ms）の波形データが100ms刻みで記録されています。

波形は、1~100行が「正常な波形」、101~125行が「正常と違う波形」の想定で作られています。

※波形データに対して、今回は固定区間ごとのサンプリングを用いていますが、他にもデータセットを工夫する手法がございます。（ページ末に記載）

【予測する列（目的変数の設定）について】

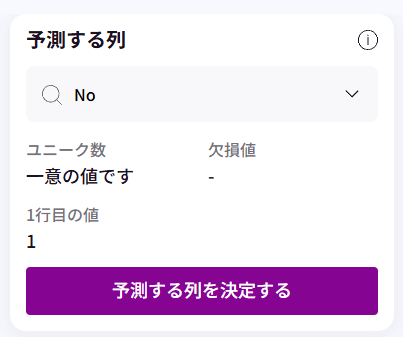
ClusterFlow（クラスタリング）は「教師なし学習」に分類される手法のため、学習時に予測する列（目的変数）は使用しません。
そのため、予測する列には**「各レコードを識別するための一意の連番」**を指定しても問題ありません。

今回のデモデータセットでは、「No」列がこの役割を担います。
学習には影響しないため、識別用としてそのままご利用いただけます。

【ClusterFlowのレシピについて】

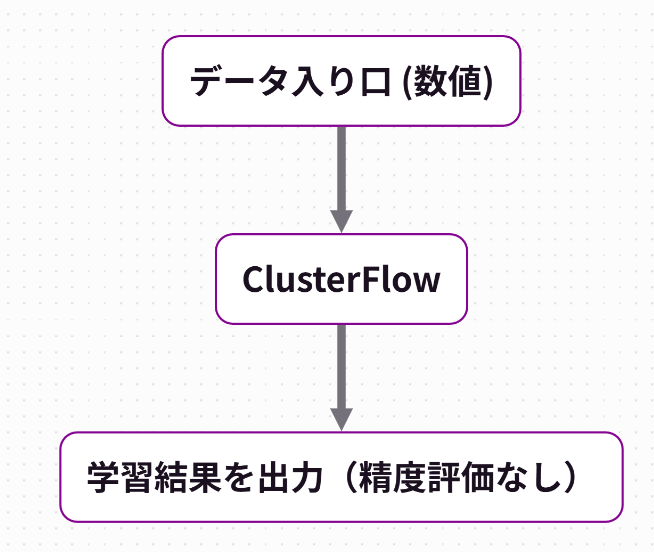
レシピの構成は右図の通りです。
終点は「学習結果を出力（精度評価なし）」を配置する必要があります。

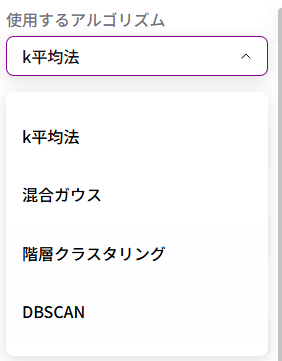
アルゴリズムは「k平均法」「混合ガウス」「階層クラスタリング」「DBSCAN」の４つに対応しています。

＜k平均法 / 混合ガウス / 階層クラスタリング＞のパラメータ

クラスター数の最小値※1 / クラスター数の最大値 / 次元圧縮の次元※2

　※1）似たもの同士のグループの最小個数を決めます。最大値はその逆です。
　※2）情報（特徴量）の意味を保ちながら少ない情報にまとめてくれます。例えば、次元を２にすると、２つの次元に纏めます。

＜DBSCAN＞のパラメータ

DBSCANの半径 / DBSCANのコア点の最小個数※3

　※3）DBSCANの半径 / DBSCANのコア点の最小個数がわからない場合は「自動」がおすすめです。

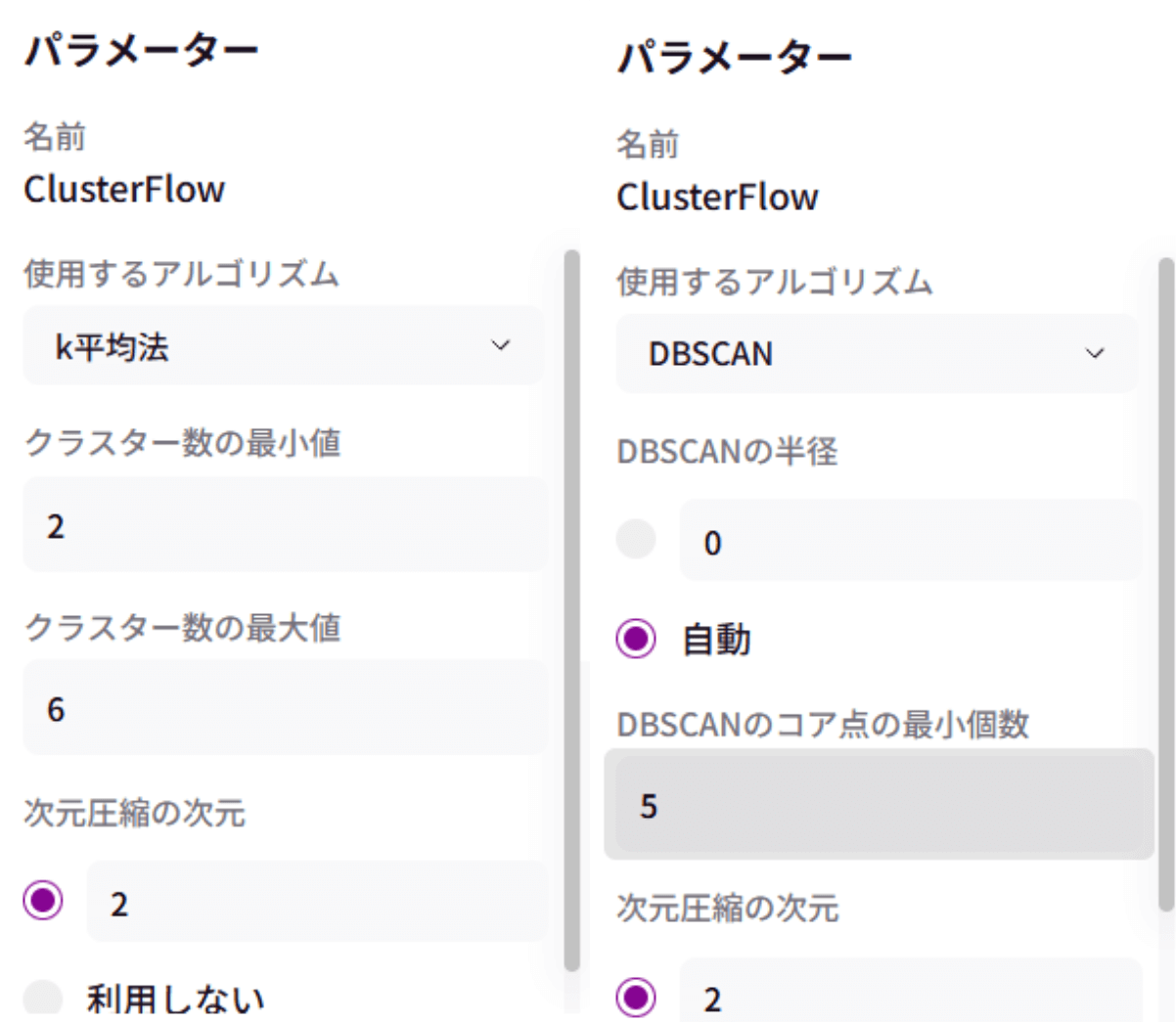
【k平均法/混合ガウス/階層クラスタリング】

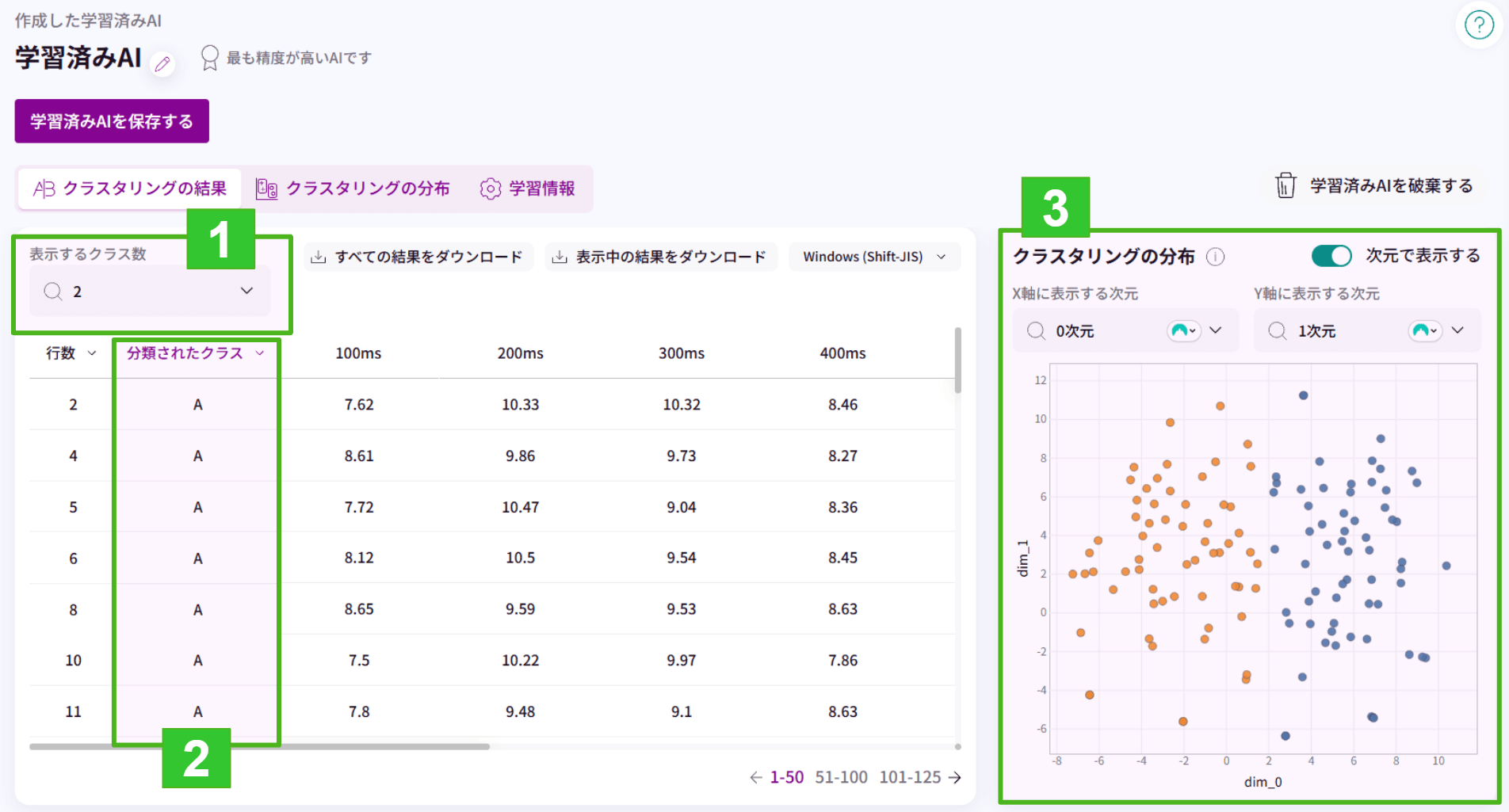
１．表示するクラス数を変更することができます。

２．表示するクラス数に合わせた「分類されたクラス」が表示されます。（アルファベットで表記されます）

３．クラスタリングの分布が表示されます。（X軸とY軸に列の設定が必要です）

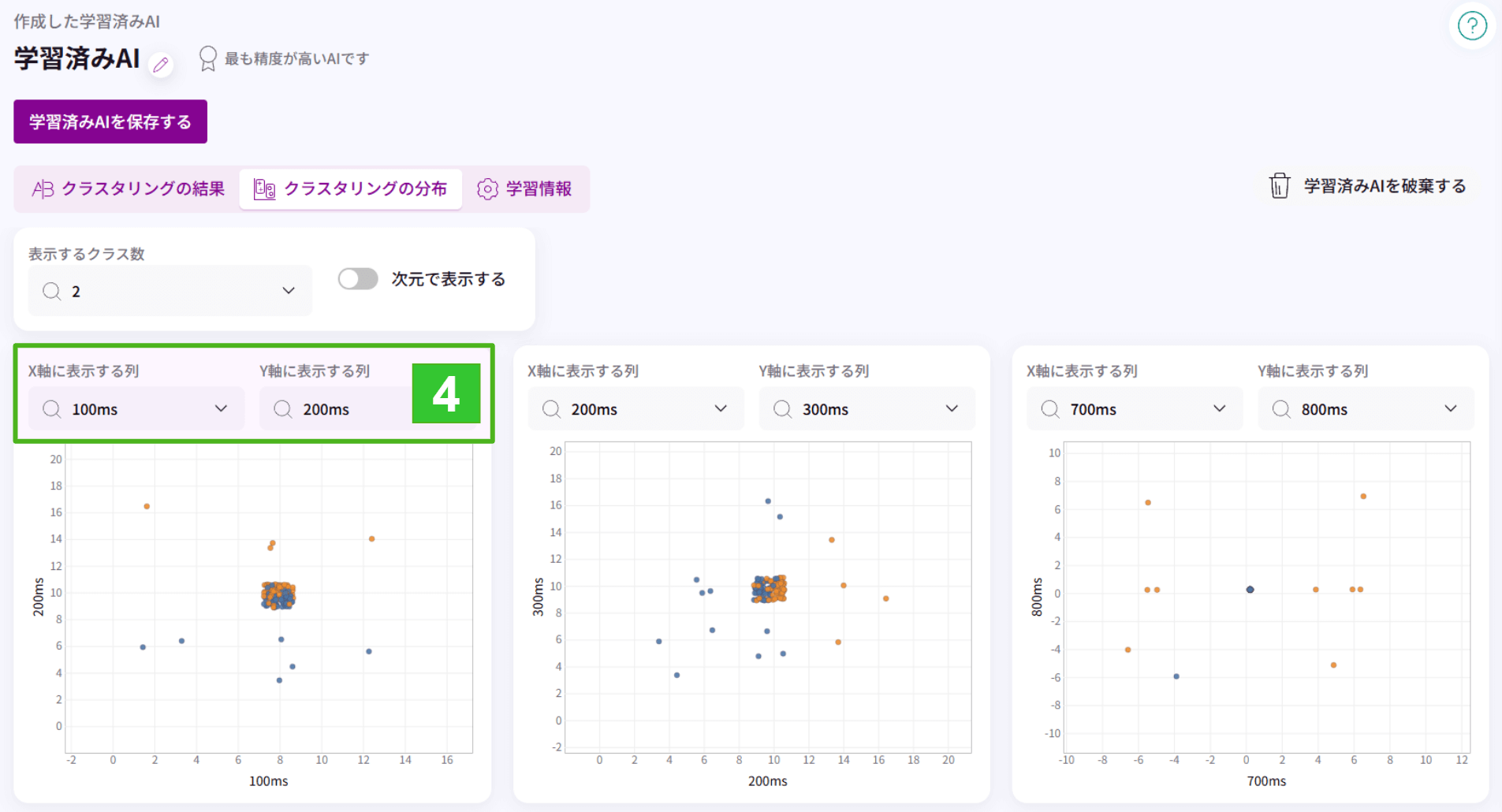
４．クラスタリングの分布のみのタブで、クラスタリングの分布のみを表示する画面です。X軸に表示する列とY軸の表示する列を設定することで、クラスタリングの分布図が表示されます。

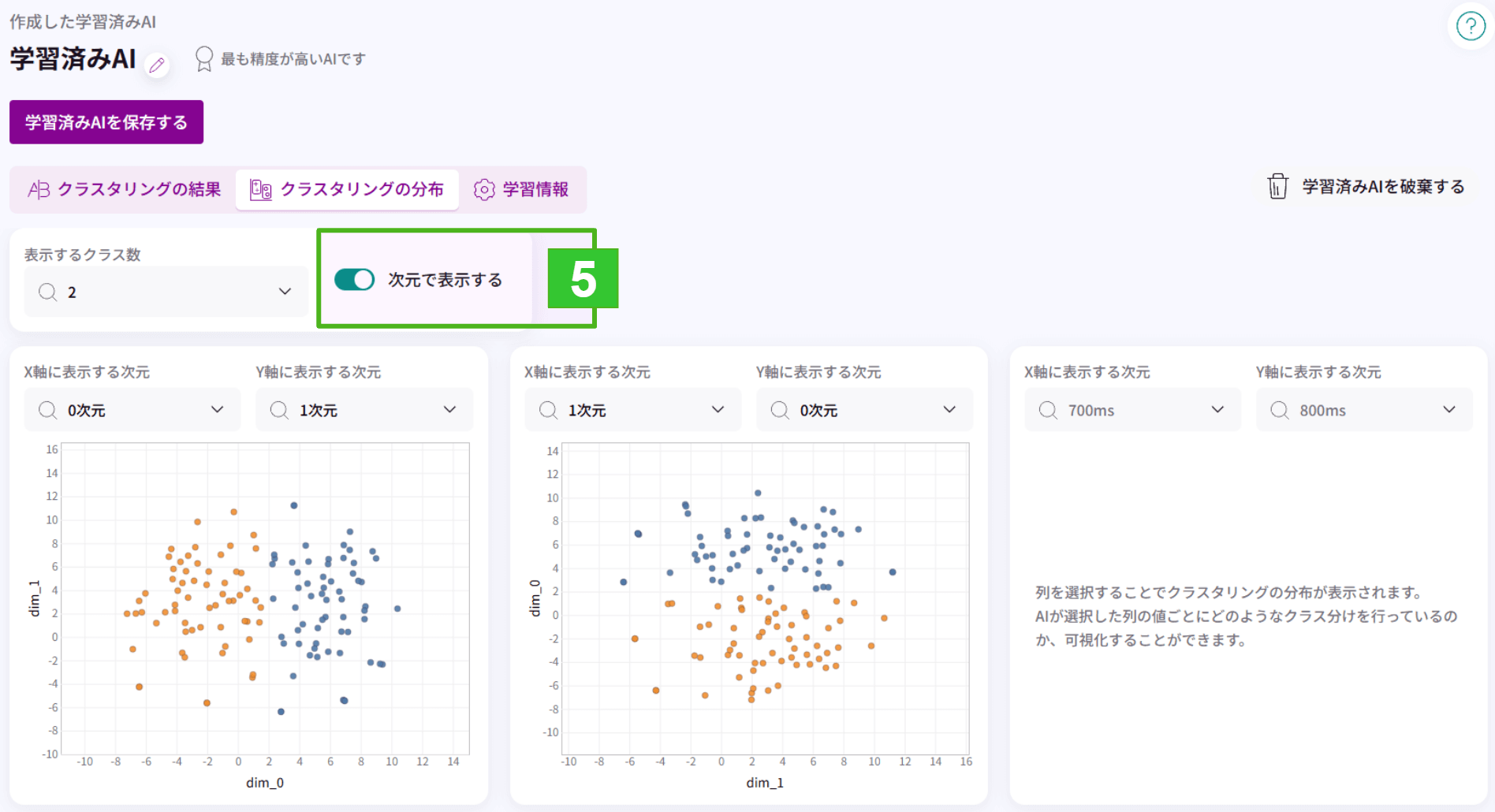
５．次元で分布を表示することができます。

【DBSCAN】

基本的な操作・使い方は【k平均法/混合ガウス/階層クラスタリング】と変わりません。
仕組みが大きく違うため、表示される内容に違いがあります。

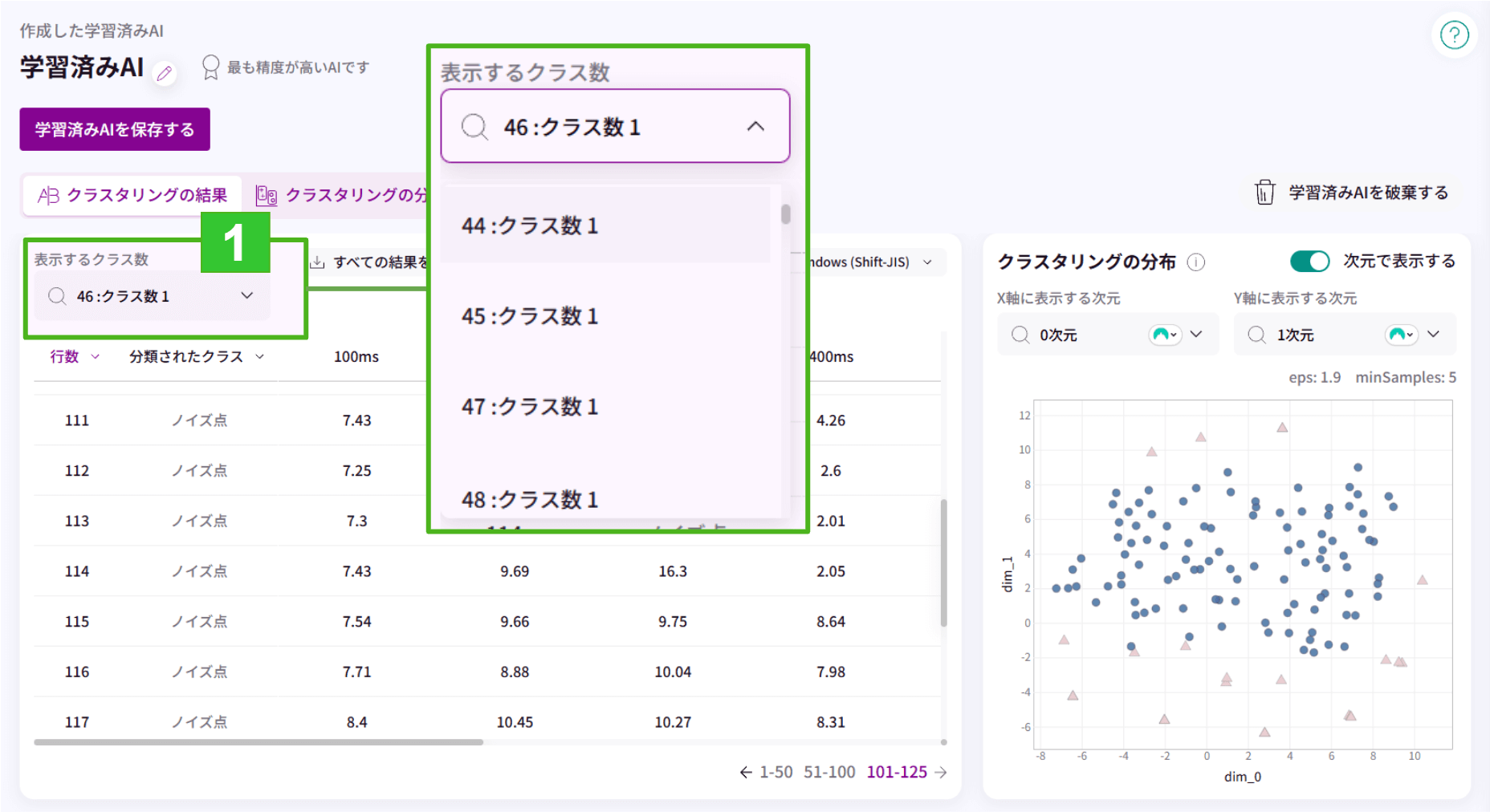
１．「表示するクラス数」で、それぞれの探索内容を選択して調節し、表示することができます。
※DBSCANの半径 / DBSCANのコア点の最小個数を「自動」にした場合

　ノイズと思われる箇所がノイズ点となるように調整します。

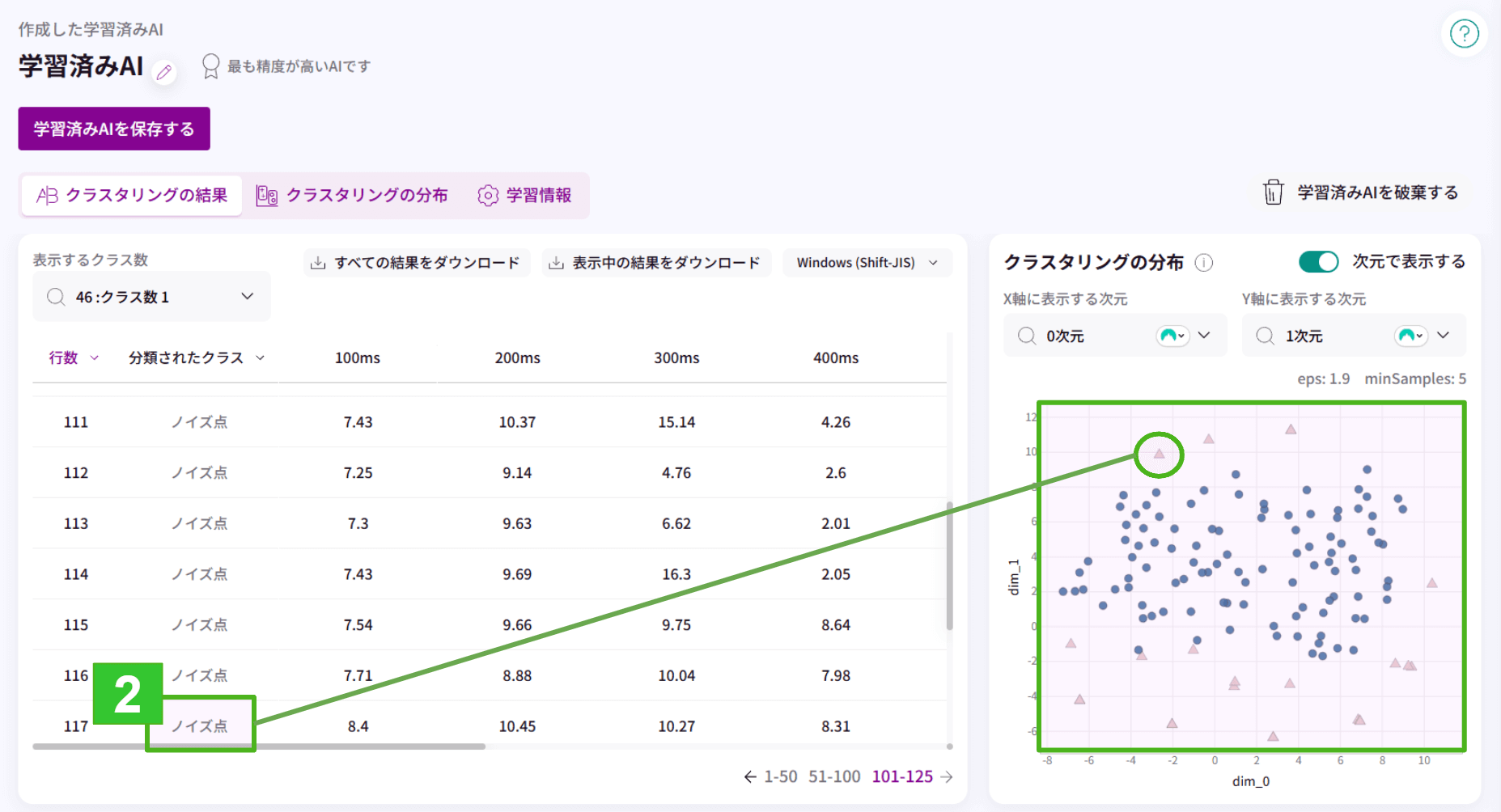
２．今回のデータセットでは100行～125行が異常値であるだろうと想定しているため、そこにノイズ点を調整しました。
ノイズ点＝特定の点（今回の場合、異常値）として扱うことができます。

その他の波形データへの手法（一部ご紹介）

🔶スライディングウィンドウ処理

波形の一部分（例：5点分）を少しずつずらして取り出す方法です。
波形を一定区間ごとに少しずつずらして分割します。
たとえば「連続する100ms × 5回分のデータ」を1つのまとまりとして分析します。

➡ 異常検知・状態遷移検出に向いている

➡ 時間的なパターンの変化を捉えやすくなる（変化の局所的パターンを捉えやすくなる）

➡ データ量が増える

🔶フーリエ変換・スペクトル変換

波形データを「どんな周期成分が含まれているか」という視点で数値化します。(波形（時系列）→ 周波数成分に変換（FFTなど）)
例えば「ゆっくりした波」「細かく振動している波」が分かるようになります。

➡ 周期性・異常検知に強い（音響分析・周期性のある異常検知に向いている）

➡ 周波数成分が可視化される

➡ 解釈がやや専門的、波形の直感性が失われることも

🔶統計特徴量の抽出

波形全体の特徴（例：平均値、最大値、ばらつき、形のゆがみなど）を数値化します。
データの「形や傾向」をざっくり掴みやすく、モデル学習にも向いています。

➡ 分類・回帰のモデルに使いやすい

➡ 数値的に安定／解釈しやすい

➡ 波形そのものの形状は失われる

※データへの処理対応の詳細につきましては、ベーシックプラン（https://www.matrixflow.net/matrixflow/contact-basic-plan）の「データサイエンティストサポート」にてご案内しております。ご希望の際は、お気軽にお問い合わせください。

MatrixFlowマニュアル